Комбинаторика является древнейшей и, возможно, ключевой ветвью математики. Всякому анализу предшествует комбинаторное рассмотрение, всякая серьёзная теория имеет комбинаторный аналог.
Комбинаторика располагает столь многообразными методами, решает столь разнообразные задачи, что трудно чётко обозначить её границы. Условно в комбинаторной теории можно выделить следующие три большие части (см. схему):
- Теорию конфигураций, включающую блок - схемы, группы подстановок, теорию кодирования.
- Теорию перечисления, содержащую производящие функции, теоремы обращения и исчисление конечных разностей.
- Теорию порядка, включающую конечные упорядоченные множества и решётки, матрицы и теоремы существования, подобные теоремам Холла и Рамсея.
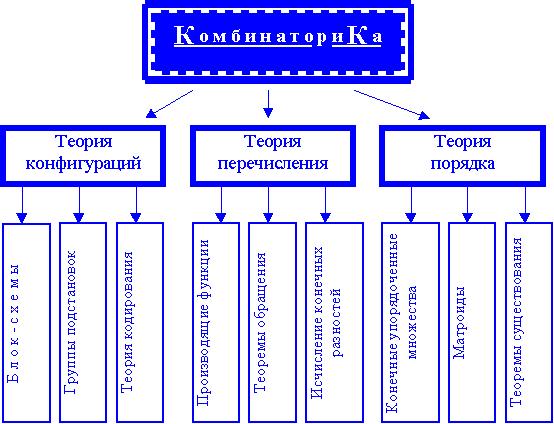
Следует ещё раз подчеркнуть в высшей степени условный характер представленной схемы. Повсеместно можно наблюдать взаимную связь перечисленных разделов комбинаторики. Например, перечислительная комбинаторика рассматривает задачи, относящиеся и к конфигурациям, и к упорядоченным множествам.
Теория конфигураций и теория перечисления
Теория конфигураций является традиционным и наиболее разработанным разделом комбинаторики. Теория конфигураций рассматривает задачи выбора и расположения элементов некоторого, обычно конечного, множества, в соответствии с заданными правилами. Перечислительная комбинаторика основным методом исследования провозгласила метод производящих функций, используя который было доказано громадное число комбинаторных тождеств.
Элементарными комбинаторными конфигурациями являются сочетания, размещения, перестановки. Для подсчёта числа этих конфигураций используются правила суммы и произведения.
Правило суммы:
Если элемент A можно выбрать m способами, а элемент B можно выбрать k способами, то выбор элемента A или B можно осуществить m + k способами.
Правило суммы можно перефразировать на теоретико-множественном языке. Обозначим через | A | число
элементов множества A, через A 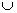 B - объединение множеств A и B, через AxB - декартово произведение
множеств A и B. Тогда для непересекающихся множеств A и B выполняется равенство:
B - объединение множеств A и B, через AxB - декартово произведение
множеств A и B. Тогда для непересекающихся множеств A и B выполняется равенство:
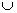 B | = | A | + | B |.
B | = | A | + | B |.
Обобщением правила суммы является правило произведения.
Правило произведения:
Если элемент A можно выбрать m способами, а после каждого выбора элемента A элемент B можно выбрать k способами, тогда, упорядоченную пару элементов (A, B) можно выбрать m*k способами.
Правило произведения можно распространить на выбор последовательности
(x1, x2, …, xn)
произвольной конечной длины n.
На теоретико-множественном языке правило произведения формулируется так: | Aх
B | = | A |
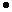 | B |.
| B |.
Размещения.
Назовём множество, содержащее n элементов, n-множеством.
Последовательность (x1, x2, …, xk ) длины k без повторяющихся элементов из элементов данного n-множества назовём k-размещением.
Обозначим символом 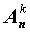 число размещений из n по k элементов (от фран. "arrangement" - размещение).
Используя правило произведения, вычислим число
число размещений из n по k элементов (от фран. "arrangement" - размещение).
Используя правило произведения, вычислим число 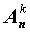 .
.
Пусть произвольное размещение длины k имеет вид:
Элемент x1 можно выбрать n способами. После каждого
выбора x1 элемент x2 можно выбрать
(n - 1) способами. После каждого выбора элементов x1 и
x2 элемент x3 можно выбрать
(n - 2) способами, и т.д. После каждого выбора элементов x1
, x2, …, xk-1 элемент xk можно выбрать
(n - (k - 1)) = (n - k + 1) способами. Тогда, по правилу произведения, последовательность
(x1; x2; , …, xk ) можно выбрать
числом способов, равным
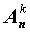 (1.1)
(1.1)
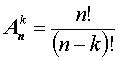 .
(1.2)
.
(1.2)
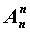 есть число
Pn перестановок из n элементов
есть число
Pn перестановок из n элементов
Сочетания.
k-подмножество данного n-множества называется k-сочетанием.
Обозначим через 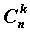 число k-сочетаний из данных n
элементов. Формулу для числа
число k-сочетаний из данных n
элементов. Формулу для числа 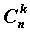 получим, рассуждая следующим образом. Если каждое сочетание упорядочить всеми
возможными способами, то получим все k-последовательностей из n элементов, без повторений,
то есть все k-размещения.
получим, рассуждая следующим образом. Если каждое сочетание упорядочить всеми
возможными способами, то получим все k-последовательностей из n элементов, без повторений,
то есть все k-размещения.
Иными словами, 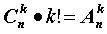
Откуда: 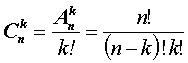 (1.3)
(1.3)
или 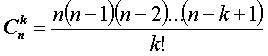
Предполагая, что n и k - целые положительные числа и 0!=1,
сформулируем основные свойства сочетаний.
Основные свойства сочетаний.
- Условились, что
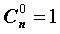
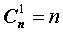
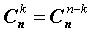
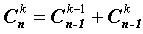
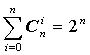
Пример. В корзине находятся 20 орехов, из которых 7 грецких. Наудачу выбирают 5 орехов. Найти вероятность того, что среди выбранных орехов содержатся 2 грецких.
Решение. Число исходов опыта 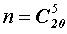 .
Случайное событие A - среди пяти выбранных
орехов содержатся 2 грецких ореха. Число исходов, благоприятствующих событию A, равно:
.
Случайное событие A - среди пяти выбранных
орехов содержатся 2 грецких ореха. Число исходов, благоприятствующих событию A, равно:
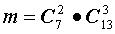 .
Искомая вероятность
.
Искомая вероятность 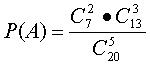 .
.
Задачи.
- Найти вероятность того, что случайно выбранное 5-значное (десятичное) число не содержит цифры 5.
- Предприятие располагает 5 вакансиями для мужчин, 5 вакансиями для женщин и 4 вакансиями для работников любого пола. В отдел кадров предприятия обратилось 20 человек, среди которых 12 мужчин и 8 женщин. Сколькими способами предприятие может заполнить имеющиеся вакансии?
- В классе 25 учеников, из которых 13 юношей и 12 девушек. Сколькими способами 25 учеников могут встать в шеренгу так, чтобы юноши после удаления из строя девушек, оказались построенными по росту; аналогично девушки после удаления из строя юношей оказались построенными по росту?
В современной литературе наиболее употребителен для обозначения числа k-сочетаний из
n элементов символ 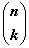 ,
n называют верхним индексом, k - нижним индексом.
,
n называют верхним индексом, k - нижним индексом.
Используя свойства сочетаний 1, 2, 4, составим таблицу1.
 |
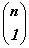 |
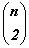 |
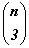 |
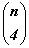 |
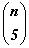 |
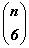 |
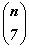 |
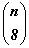 |
 |
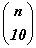 |
|
Заметим, что Блез Паскаль называл числовой треугольник, начало которого содержится в таблице1,
арифметическим. Паскаль посвятил свойствам арифметического треугольника основополагающий
"Трактат об арифметическом треугольнике" (1654). Справедливости ради, стоит упомянуть, что биномиальные
коэффициенты были хорошо известны в Азии за много веков до рождения Паскаля. В Италии треугольник
Паскаля называют треугольником Тартальи.
Сочетания имеют многочисленные интерпретации и приложения.
Сочетания 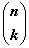 являются биномиальными коэффициентами в разложении бинома
являются биномиальными коэффициентами в разложении бинома
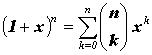 (1.4)
(1.4)
В этой интерпретации индексы могут принимать вещественные значения. Используя свойства биномиальных
коэффициентов (при разных ограничениях на выбор верхних и нижних индексов), доказано громадное число
комбинаторных тождеств, составивших самостоятельный раздел комбинаторной математики. В частности, из
формулы 1.4 при x = 1, получим 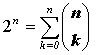 ,
при
,
при
x = -1, n > 0, получим 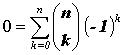 ,
продифференцировав равенство 1.4, получим при x = 1,
,
продифференцировав равенство 1.4, получим при x = 1,
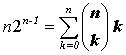 и т.д.
и т.д.
Существует тесная связь между подмножествами множества и разложениями целого (положительного)
числа. Разложение n есть представление числа n в виде упорядоченной суммы
положительных целых чисел. Например, существует восемь разложений числа 4, именно:
1+1+1+1 3+1
2+1+1 1+3
1+2+1 2+2
1+1+2 4
Если разложение 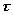 содержит в точности k слагаемых, то говорят, что
содержит в точности k слагаемых, то говорят, что 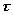 имеет
k частей и называется k-разложением. Для k-разложения
имеет
k частей и называется k-разложением. Для k-разложения
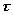 числа n: a1 + a2 + …+ an - определим
числа n: a1 + a2 + …+ an - определим
(k - 1)-подмножество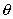 (
( 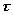 ), (n - 1)-множества {1, 2, …, n-1},
формулой.
), (n - 1)-множества {1, 2, …, n-1},
формулой.
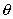 (
(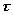 )
={ a1, a1 + a2,…,
a1 + a2 +…+ ak-1 }
(1.5)
)
={ a1, a1 + a2,…,
a1 + a2 +…+ ak-1 }
(1.5)
Эта формула устанавливает биекцию между всеми k-разложениями числа n и
(k - 1)-подмножествами (n - 1)-множества.
Следовательно, существует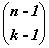 k-разложений числа n и 2n-1
разложений числа n. Биекцию
k-разложений числа n и 2n-1
разложений числа n. Биекцию 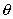 часто схематично изображают строкой, состоящей из n
точек и k - 1 разделяющей вертикальной черты. Точки разделились по k
линейно упорядоченным "купе"; числа точек в "купе" соответствуют слагаемым в k-разложении
числа n. Например, строка
часто схематично изображают строкой, состоящей из n
точек и k - 1 разделяющей вертикальной черты. Точки разделились по k
линейно упорядоченным "купе"; числа точек в "купе" соответствуют слагаемым в k-разложении
числа n. Например, строка 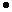 |
|
 |
|  |
|  |
|
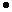
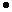 |
|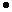
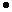 соответствует разложению 1+2+1+1+3+2.
Другая проблема, тесно связанная с разложениями, есть задача подсчёта числа N(n,k)
решений уравнения
соответствует разложению 1+2+1+1+3+2.
Другая проблема, тесно связанная с разложениями, есть задача подсчёта числа N(n,k)
решений уравнения
Неотрицательные целые решения уравнения 1.6 называются слабыми k-разложениями числа n. Число неотрицательных целых решений уравнения 1.6 равно числу положительных решений уравнения
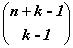 .
.
Если k-сочетание содержит повторяющиеся элементы, то такое k-сочетание
называют
k-мультимножеством. Число всех k-сочетаний с повторениями из
данного n-элементного множества обозначим через 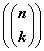 , где
, где
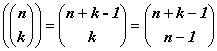 (1.7)
(1.7)
Сочетание 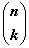 можно интерпретировать, как распределение
элементов n-множества S между двумя категориями, первая из которых
содержит k элементов, вторая содержит n - k элементов. Обобщим это
представление. Пусть
(a1, a2, …, am)-
последовательность неотрицательных целых чисел, сумма которых равна n. Рассмотрим
m категорий
C1, C2, … Cm.
можно интерпретировать, как распределение
элементов n-множества S между двумя категориями, первая из которых
содержит k элементов, вторая содержит n - k элементов. Обобщим это
представление. Пусть
(a1, a2, …, am)-
последовательность неотрицательных целых чисел, сумма которых равна n. Рассмотрим
m категорий
C1, C2, … Cm.
Обозначим символом 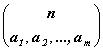 (1.8)
(1.8)
число способов распределения n элементов среди категорий
C1, C2, … Cm
так, чтобы категории Ci принадлежало точно
ai элементов. Тогда 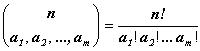 (1.9)
(1.9)
Блок-схемы
Комбинаторные конфигурации наиболее общего вида были исследованы в 30-е годы XX столетия и были названы блок-схемами (block design). Блок-схемы состоят из наборов элементов, называемых блоками. Выбор элементов и пар элементов в блоки подчиняются определённым правилам.
Уравновешенной неполной блок-схемой называется такое размещение v различных элементов
по b блокам, что каждый блок содержит точно k различных элементов,
каждый элемент появляется точно в k различных блоках и каждая пара различных элементов
ai , aj появляется точно в
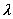 блоках.
блоках.
Множество всех 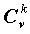 сочетаний из v элементов по k, взятых в качестве блоков,
образует полную блок-схему. Часть этих сочетаний, в которых каждая пара ai,
aj появляется одно и то же число раз, является неполной, но уравновешенной
блок-схемой. Между пятью параметрами блок-схемы выполняются следующие два соотношения:
сочетаний из v элементов по k, взятых в качестве блоков,
образует полную блок-схему. Часть этих сочетаний, в которых каждая пара ai,
aj появляется одно и то же число раз, является неполной, но уравновешенной
блок-схемой. Между пятью параметрами блок-схемы выполняются следующие два соотношения:
r (k - 1) = (v - 1) (1.11)
Частным случаем блок-схем являются так называемые конечные плоскости. Выберем конечное множество P. Элементы из P назовём точками. Некоторые подмножества из P назовём прямыми. Пусть отношение инцидентности между точками и прямыми удовлетворяет следующим геометрическим аксиомам.
- На каждой прямой лежит n точек B.
- Через каждую точку проходят n прямых.
- Любые две прямые пересекаются в одной точке.
- Через любые две точки проходит единственная прямая.
- Существуют 4 точки неколлинеарные по три.
Тогда конечное множество P точек и множество L прямых образует конечную проективную плоскость.
Пример:
P = {1, 2, 3, 4, 5,
6, 7}.
L = {l1, l2, l3,
l4, l5,
l6, l7}
l1 = {1, 2, 3}, l2 = {3, 4, 5}, l3 = {1, 5, 6},
l4 = {1, 4, 7}, l5 = {2, 5, 7},
l6 = {3, 6, 7}, l7 = {2, 4, 6}.